March 17, 2020 python STEM gráficas
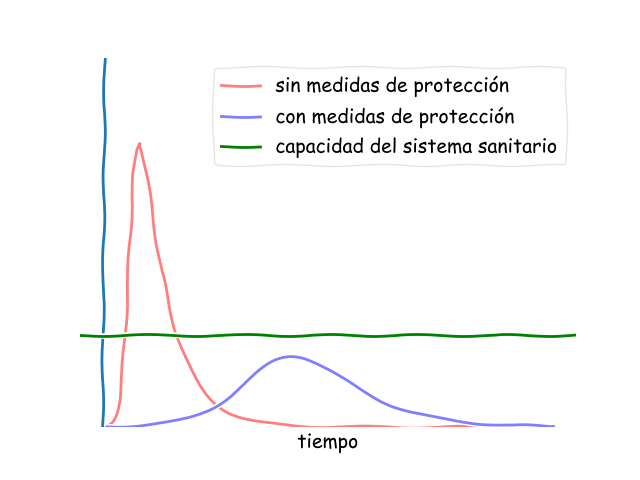
Aplanar la curva
Seguramente estos días habréis oído la expresión aplanar la curva, pero ¿realmente sabéis lo que significa? En esta entrada vamos a explicarlo y de paso os explicaremos como representar gráficas con Python.
Ralentizar la expansión
El objetivo ideal contra una epidemia infecciosa es atajarla completamente. Pero cuando el agente patógeno es muy contagioso, atajarla resulta imposible y el objetivo debe ser ralentizar su expansión. De esta forma, tenemos menos personas contagiadas a la vez y los recursos de los que disponemos para luchar contra la enfermedad y sus consecuencias no se ven sobrepasados.
¿De qué recursos hablamos?
- Plazas hospitalarias y personal sanitario, para que todos los enfermos puedan ser atendidos.
- Científicos e investigadores, para que puedan estudiar la enfermedad y buscar curas o formas de detenerla.
- Servicios básicos, para que tengamos comida, medicinas, recogida de basuras.
Si toda la población enfermase a la vez no sería posible disponer de estos recursos para todos. Ralentizar la expansión nos permite seguir funcionando como sociedad.
Crecimiento exponencial
Antes hemos dicho que algunos patógenos son muy contagiosos. Pongamos un ejemplo imaginario, el virus de la ejemplitis.
La ejemplitis es una enfermedad muy contagiosa; siempre que una persona que la sufre toca a otra persona, ésta queda contagiada. Supongamos que cada persona se toca con otras dos personas cada hora y veamos qué ocurre con el número de afectados.
| horas | nuevos contagios | total contagios |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 6 | 9 |
| 4 | 18 | 27 |
| 5 | 54 | 81 |
| 6 | 162 | 243 |
Simulemos esta progresión de contagios con Python (usamos el operador Walrus no olvidéis utilizar la versión 3.8 de Python como mínimo). En este primer ejemplo vamos a crear una lista llamada simulacion en la que almacenaremos tuplas con los valores de hora, número de nuevos contagios y número total de contagios. En cada iteración del bucle while, cada uno de los infectados causa tantas nuevas infecciones como la tasa de contagio. Para representar los datos en forma de tabla, usamos el paquete tabulate, recordad instalarlo antes de ejecutar el ejemplo con pip install tabulate. La función tabulate nos devuelve el texto formateado y con las cabeceras especificadas en headers que pasamos a print.
from tabulate import tabulate
total_infectados = 1
horas_de_simulacion = 24
horas_transcurridas = 0
tasa_de_contagio = 2
headers = ["hora", "nuevos", "total"]
simulacion = [(0, 1, 1)]
while (horas_transcurridas := horas_transcurridas + 1) < horas_de_simulacion:
nuevos_infectados = total_infectados * tasa_de_contagio
total_infectados += nuevos_infectados
simulacion.append((horas_transcurridas, nuevos_infectados, total_infectados))
print(tabulate(simulacion, headers))
Un crecimiento de este tipo se denomina exponencial ya que, como puedes ver los valores de contagios crecen muy rápidamente; por ejemplo sólo hacen falta 16 horas para que se contagie una población similar a la de España.
hora nuevos total
------ ----------- -----------
0 1 1
1 2 3
2 6 9
3 18 27
4 54 81
5 162 243
6 486 729
7 1458 2187
8 4374 6561
9 13122 19683
10 39366 59049
11 118098 177147
12 354294 531441
13 1062882 1594323
14 3188646 4782969
15 9565938 14348907
16 28697814 43046721
17 86093442 129140163
18 258280326 387420489
19 774840978 1162261467
20 2324522934 3486784401
21 6973568802 10460353203
22 20920706406 31381059609
23 62762119218 94143178827
Ahora bien, tenemos que poner los resultados en contexto:
- El virus de la ejemplitis es tan contagioso que si te tocan te contagias indefectiblemente. Con enfermedades reales no es tan sencillo resultar contagiado.
- En nuestra simulación, cada persona busca a 2 personas para contagiar cada hora. Por suerte, la mayor parte de los humanos no nos comportamos como zombies ávidos de extender plagas e intentamos aislarnos y evitar contagiar a los demás cuando sabemos que estamos infectados.
¿Qué ocurriría si la tasa de contagio fuese mayor? Probad el el programa de nuevo con una tasa de contagio 5.
Por fortuna la ejemplitis no es una enfermedad real y nuestra simulación es muy simplista, pero nos sirve para entender un crecimiento exponencial. Los datos que hemos visto en forma de tabla son interesantes, pero es más sencillo interpretarlos con el uso de gráficas.
Gráficas en dos dimensiones
Una gráfica en dos dimensiones es una representación visual que nos permite comprender fácilmente la relación entre dos magnitudes. Hagamos un ejemplo en Python para visualizar el coste de tener encendida una bombilla.
Para dibujar una gráfica usamos el paquete matplotlib, recordad instalarlo antes de ejecutar el ejemplo con pip install matplotlib. Dentro del paquete, la función plot(x,y,format) nos sirve para dibujar una gráfica pasando los valores de las magnitudes en las listas x e y. El formato es una cadena, que por defecto es b-, que quiere decir color azul (b de blue) y conectado los puntos por líneas sólidas(-).
En nuestro ejemplo vamos a usar una bombilla de 25 vatios, con un coste de la electricidad de 0,13 euros por kilovatio. Con la función coste calculamos cuanto cuesta la electricidad dependiendo del número de horas y la potencia de la bombilla. Con un bucle while rellenamos las dos listas con los valores de las magnitudes tiempo y consumo y finalmente representamos la gráfica pasando a la función plot las dos listas y añadiendo o al formato para que dibuje círculos en los puntos. Para que nuestra gráfica se pueda entender mejor añadimos etiquetas a los ejes con xlabel y ylabel, ponemos un título a la gráfica con title y mostramos la rejilla con grid.
import matplotlib.pyplot as plt
potencia_bombilla_vatios = 25
euros_por_kilovatio = 0.13
horas = list()
consumos = list()
hora = 0
def coste(vatios, horas):
kilovatios = vatios / 1000
coste = euros_por_kilovatio * kilovatios * horas
return coste
while (hora := hora + 1) < 24:
horas.append(hora)
consumos.append(coste(potencia_bombilla_vatios, hora))
plt.plot(horas, consumos, "bo-")
plt.xlabel("horas encendida")
plt.ylabel("coste en €")
plt.title("coste de la electricidad por horas de una bombilla")
plt.grid(True)
plt.show()
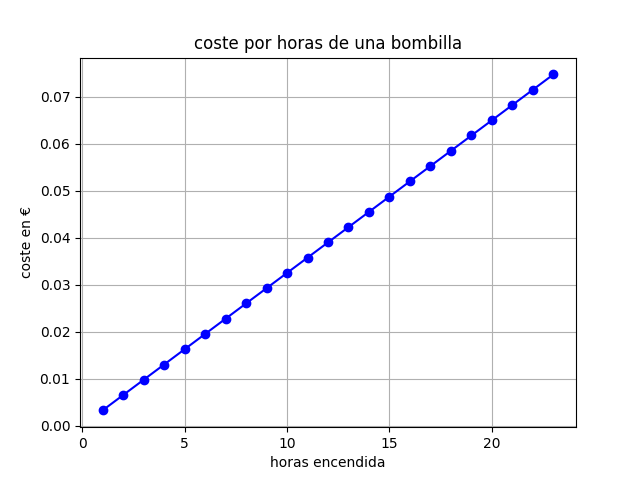
La gráfica resultante nos resulta muy útil para entender de un vistazo que si dejo la bombilla encendida durante 15 horas gastaré unos 5 céntimos de euro.
Una explosión incontrolada
Ahora que ya sabemos cómo dibujar una gráfica vamos a representar la simulación de contagios. Fijaos que ahora vamos a guardar las listas con las magnitudes dentro de un diccionario llamado simulacion. De esta forma podemos utilizar la función plot de otra forma, en la que la variable data que se le pasa es un diccionario y especificamos las listas que se usan en para pintar pasando su nombre.
import matplotlib.pyplot as plt
total_infectados = 1
horas_de_simulacion = 24
horas_transcurridas = 0
tasa_de_contagio = 2
# Diccionario que contiene 3 listas
simulacion = {"horas": [0], "nuevos": [1], "total": [total_infectados]}
while (horas_transcurridas := horas_transcurridas + 1) < horas_de_simulacion:
nuevos_infectados = total_infectados * tasa_de_contagio
total_infectados += nuevos_infectados
simulacion["horas"].append(horas_transcurridas)
simulacion["nuevos"].append(nuevos_infectados)
simulacion["total"].append(total_infectados)
# Los parámetros "horas" y "total" especifican qué listas dentro de "simulacion" vamos a pintar
plt.plot("horas", "total", "bo-", data=simulacion)
plt.xlabel("horas desde el brote")
plt.ylabel("personas")
plt.title("expansión incontrolada de una epidemia")
plt.grid(True)
plt.show()
Al ejecutar el programa obtenemos esta curva en forma de letra J característica de los crecimientos exponenciales. Prestad atención a la escala del eje vertical, las unidades son 1e10 esto es, cada línea horizontal representa 20.000 millones de personas.
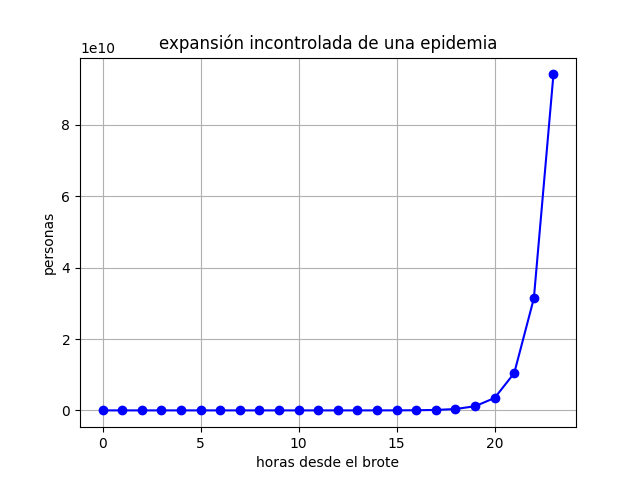
Pero que no salten las alarmas, en el mundo real esto no ocurre porque:
- No toda la población se encuentra concentrada en el mismo lugar.
- Las enfermedades no se transmiten con solo tocarnos.
- Y lo más importante, ¡las enfermedades se curan!
En efecto, tenemos que tener en cuenta dos límites para nuestro crecimiento exponencial. El primero es el límite la población y el segundo son las curaciones
Límite de población
El primer límite teórico que tendría la expansión de la epidemia es el de la población disponible: una vez nos hemos infectado todos, es imposible que crezca el número de contagios. Para simularlo, vamos a calcular el mínimo entre el total de la población y el número de casos actualizado dentro del bucle, fijaos en esta línea total_infectados = min(poblacion, total_infectados + nuevos_infectados) dentro del bucle. Además utilizamos el paquete numpy para generar el eje de tiempo con intervalos de 24 horas plt.xticks(np.arange(0, horas_de_simulacion, step=24)).
import matplotlib.pyplot as plt
import numpy as np
total_infectados = 1
dias_de_simulacion = 7
horas_de_simulacion = 24 * dias_de_simulacion
horas_transcurridas = 0
tasa_de_contagio = 0.2
poblacion = 40000000
simulacion = {"horas": [0], "nuevos": [1], "total": [total_infectados]}
while (horas_transcurridas := horas_transcurridas + 1) < horas_de_simulacion:
nuevos_infectados = total_infectados * tasa_de_contagio
total_infectados = min(poblacion, total_infectados + nuevos_infectados)
simulacion["horas"].append(horas_transcurridas)
simulacion["nuevos"].append(nuevos_infectados)
simulacion["total"].append(total_infectados)
plt.plot("horas", "total", "r-", label="total", data=simulacion)
plt.xlabel("horas desde el brote")
plt.ylabel("personas")
# Mostramos el eje horizontal con marcas desde cero hasta horas_de_simulacion en intervalos de 24 horas
plt.xticks(np.arange(0, horas_de_simulacion, step=24))
plt.axis([0, horas_de_simulacion, 0, poblacion * 1.1])
plt.title("expansión de una epidemia limitada por población")
plt.grid(True)
plt.show()
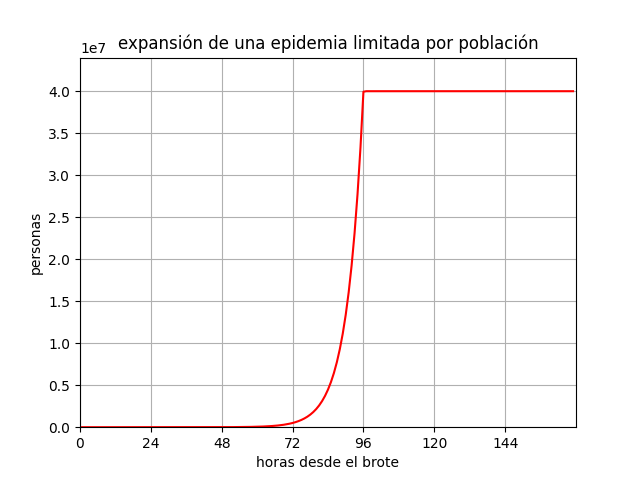
Como podéis ver en la gráfica resultante, el número de casos se mantiene constante una vez se alcanza el límite de población, y la exponencial se convierte en una línea horizontal.
¡Nos curamos!
Durante todo este rato hemos ignorado algo obvio, y es que la gran mayoría de los contagiados sanan, por lo que el número de infectados, tras alcanzar un máximo, va decreciendo según pasa el tiempo.
Existen varios modelos matemáticos para estudiar las enfermedades infecciosas y todos ellos está fuera del ámbito de esta entrada, pero para mostrar esta gráfica hemos utilizado el modelo SIR. Puedes ver el código fuente aquí
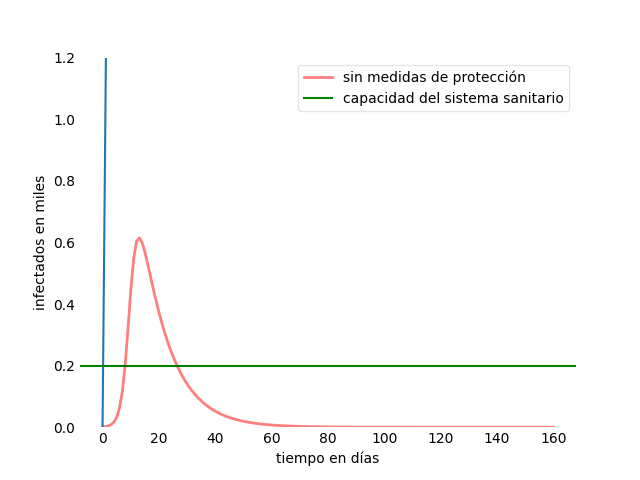
En la gráfica puedes observar que, pasado un pico inicial muy fuerte, el número de infectados comienza a decaer debido a las curaciones. El problema surge cuando el número de infectados supera las capacidades del sistema de salud, que es incapaz de atender en condiciones a todos los afectados.
Puedes jugar con el valor de contact rate, beta, para ver cuándo el número de afectados supera la capacidad del sistema
Entonces, ¿hay algo que podamos hacer para evitar este colapso? Pues sí, podemos aplanar la curva.
Aplanar la curva
Como dijimos al comienzo de esta entrada, tenemos que ralentizar el ritmo de expansión de las infecciones, de forma que el pico de la curva esté siempre por debajo de los recursos de los que dispone nuestro sistema.
En términos del modelo matemático que hemos usado se trata de reducir en lo posible la tasa de contacto. ¿Y cómo trasladamos esto al mundo real? Pues muy sencillo, quedándonos en casa. Al limitar el contacto entre personas, se ralentiza el ritmo de contagios e incluso se reduce su número total.
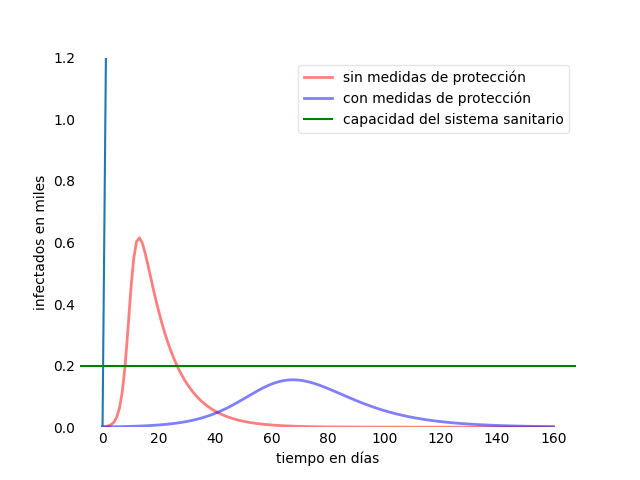
A modo de ejemplo os dejo esta gráfica que hemos generado con tasas de contacto 0,8 para el caso descontrolado y 0,2 si nos quedamos en casa. Puedes ver el código fuente aquí
Descargo de responsabilidad.
Soy ingeniero y programador, no soy médico, ni científico ni epidemiólogo, por lo que esta entrada y en especial los modelos y cifras presentadas deben ser tomadas como ejemplos ilustrativos y nunca de forma literal.
El propósito de esta entrada es ayudar a jóvenes programadores a entender el concepto de aplanar la curva a la vez que aprenden a pintar gráficas con Python y sólo puede ser entendido en dicho contexto.
Fuentes
- Flattening the Coronavirus Curve
- Why outbreaks like coronavirus spread exponentially, and to “flatten the curve”
- Pyplot tutorial
- The SIR epidemic model